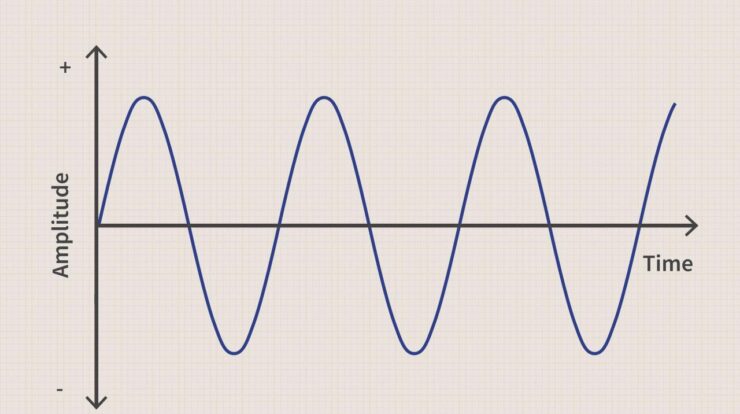
Sine meaning delves into the fascinating world of trigonometry, exploring the fundamental properties, applications, and historical significance of this crucial trigonometric function. As a cornerstone of mathematics, sine plays a pivotal role in modeling periodic phenomena, engineering applications, and our understanding of the universe.
From its mathematical definition to its real-world applications, this article provides a comprehensive overview of sine, unraveling its intricacies and showcasing its profound impact on various fields.
Sine Function
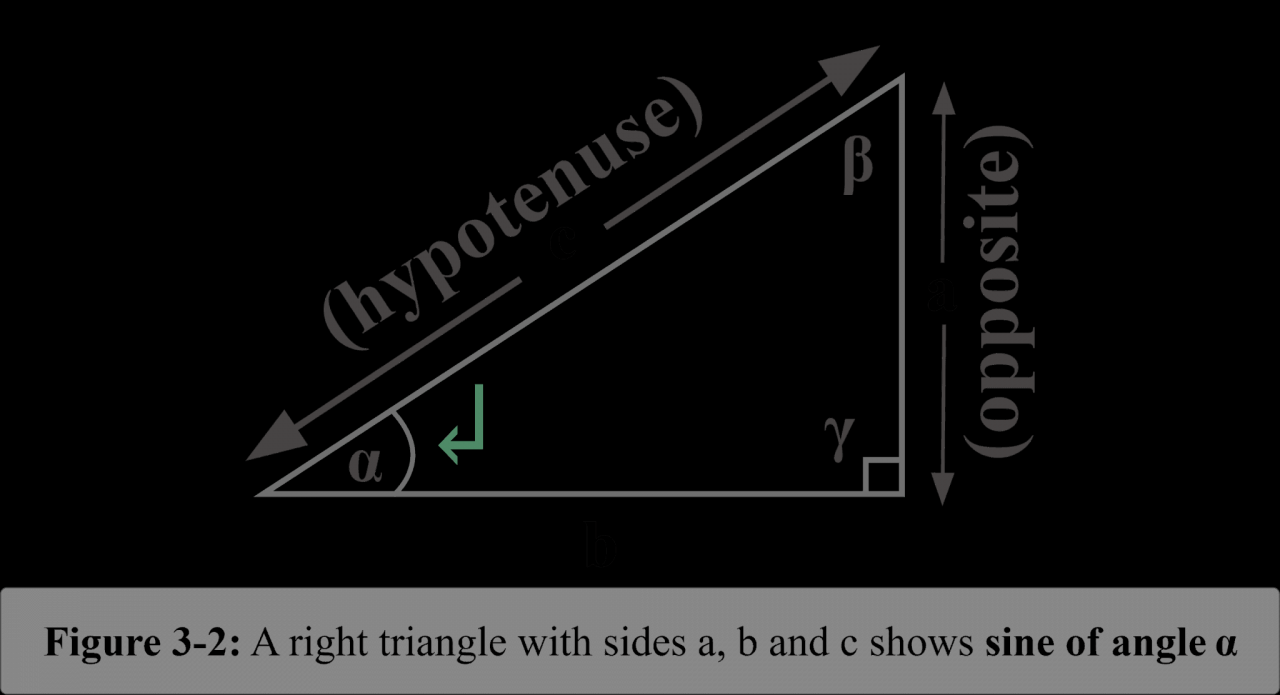
The sine function, denoted as sin(x), is a fundamental trigonometric function that describes the vertical displacement of a point on a unit circle as the angle from the positive x-axis rotates.
Mathematically, sine is defined as the ratio of the opposite side to the hypotenuse of a right triangle with an angle x at the vertex.
Properties of Sine
- Periodicity:Sine is a periodic function with a period of 2π, meaning it repeats its values every 2π units.
- Symmetry:Sine is an odd function, meaning sin(-x) = -sin(x).
- Amplitude:The amplitude of a sine wave is the maximum displacement from the center line.
- Period:The period of a sine wave is the distance between two consecutive peaks or troughs.
- Phase Shift:The phase shift of a sine wave is the horizontal displacement of the wave from its original position.
Applications of Sine
Sine is widely used in modeling periodic phenomena, such as:
- Sound waves
- Light waves
- Tidal patterns
It is also used in:
- Signal processing
- Image processing
- Engineering applications
Inverse Sine Function, Sine meaning
The inverse sine function, denoted as arcsin(x), is the inverse of the sine function.
It returns the angle whose sine is x.
Related Trigonometric Functions
Sine is related to other trigonometric functions:
- Cosine: cos(x) = sin(π/2 – x)
- Tangent: tan(x) = sin(x) / cos(x)
These relationships can be used to derive trigonometric identities.
Historical Development
The concept of sine has been known since ancient times.
The earliest known trigonometric table was compiled by Hipparchus in the 2nd century BC.
The modern definition of sine was developed by Leonhard Euler in the 18th century.
Final Thoughts
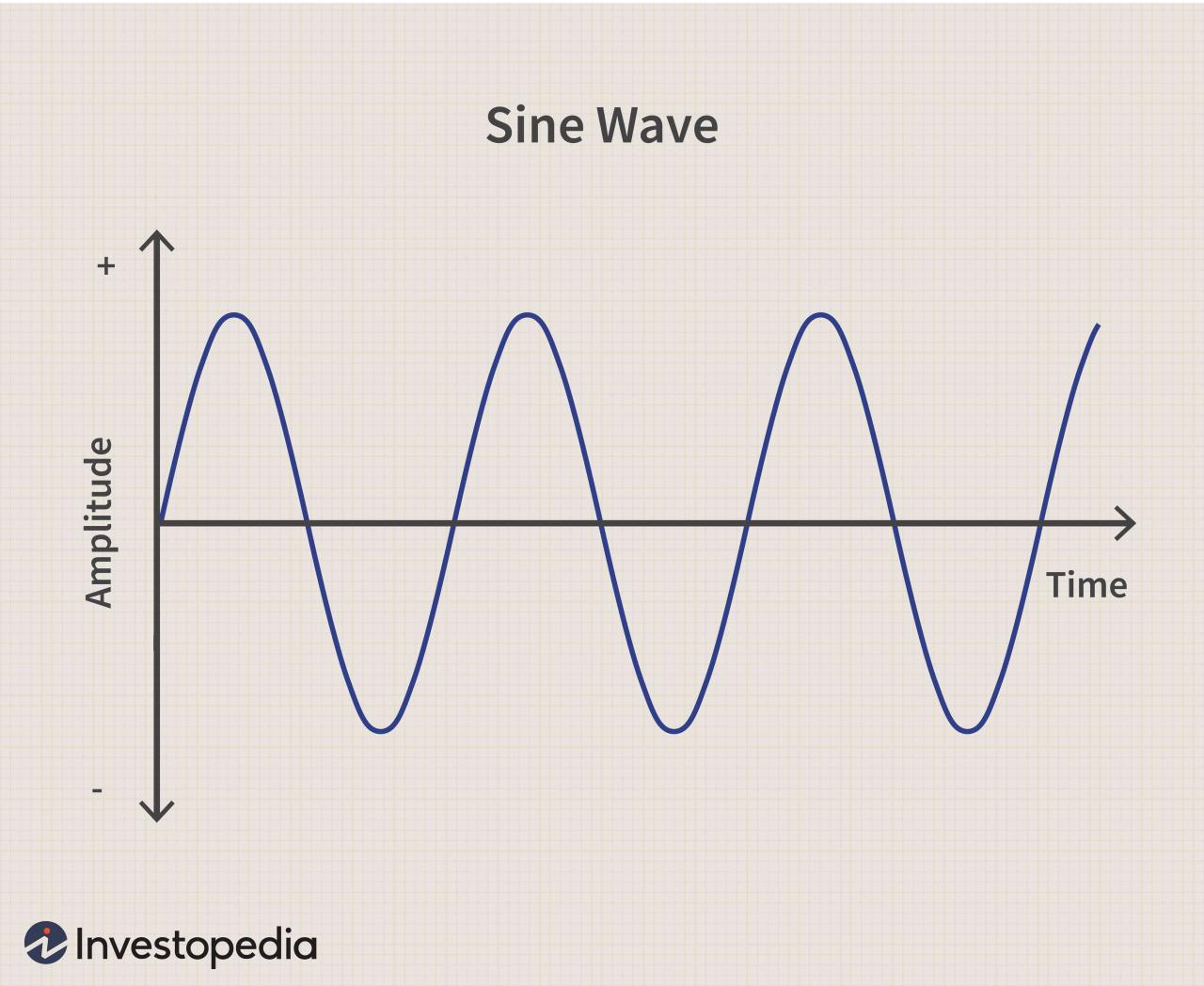
In conclusion, sine meaning stands as a testament to the power of mathematics in describing the world around us. Its versatility and widespread applications make it an indispensable tool for scientists, engineers, and anyone seeking to understand the intricacies of our universe.
FAQ Corner: Sine Meaning
What is the definition of sine?
Sine is a trigonometric function that measures the vertical component of a right triangle’s opposite side relative to its hypotenuse.
What are the properties of sine?
Sine is a periodic function with a period of 2π. It is an odd function, meaning that it is symmetric about the origin. The amplitude of a sine wave represents the maximum displacement from the equilibrium position, while the period represents the time taken for one complete cycle.
What are the applications of sine?
Sine is used in modeling periodic phenomena such as sound waves and light waves. It is also used in signal processing, image processing, and other engineering applications.